マンガワンという漫画を読めるスマホアプリがあります。知人が「ミドリノバショ」というビリヤード漫画を連載していて時々読むのですが、そこで先日「数学ゴールデン」という漫画を見つけました。

第一話を何気なく読んでいたら、高校生向けの「数学の拳（数拳）」という月刊誌に「読者の共通点」という小ネタ投稿欄があるとか。この元ネタは「大学への数学（大数）」ですね。投稿欄は「読者の接点」でした。そういえば「学力コンテスト」やったなあ。懐かしい。。。と思いながら読み進めていたら、数学の問題が出てきました。

17人それぞれが他の全員と互いに手紙のやり取りをしている。
その手紙では３つの話題のみがやりとりされている。
そして、同じ2人組の間でなされる話題は常に同じ一つのやりとりである。
このとき、互いに同じ話題の手紙のやり取りをした3人組が存在することを証明せよ。(IMO 1964)

少し考えてみたら、すんなり解けました。正しいのか確認しようと読み進めたものの、ちゃんとした説明はなく、ただラムゼーの定理がどうとか。でも、そんな定理を知らなくても（私は知りませんでした）解けるのに。この漫画（あるいは主人公）、ちょっと肩に力が入りすぎなんじゃないの？

というわけで、ここでこれを解いてみようと思います。数学の楽しさが伝わることを願いつつ。

ところで、「IMO 1964」のIMOって、InternationalなMathematicsのOlympicのこと？　と思って、国際数学オリンピックの1964年度の問題をネットで検索したら、確かにソビエト大会の第4問にこれがあったようです。

でも、大丈夫、そんなに難しくはないです。

まず、問題を理解するところから始めましょう。

「17人が互いに手紙のやりとりをしていて、その話題は３種類で、話題は変化しない。」

ということは、

「17角形の辺と全ての対角線を、3色で描き分ける」

のと同じことですね。赤と緑と青で描き分けることを想像してください。そうすると、証明すべきは、

「その中に、３辺が同じ色で描かれる三角形が（１つ以上）存在する。」

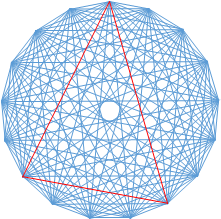
ということになります。

ここからは、

「同色の三角形を作らないようにどう頑張っても、同色の三角形がどうしてもできてしまう」

ことを示します。（「背理法」ってやつですね）

さて、どの人（頂点）も平等（対称）なので、とりあえず一つの頂点に注目しましょう。相手は16人です。

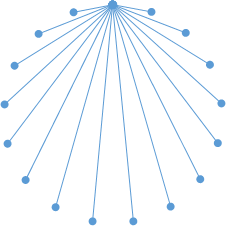
16の線を3色で描き分けるわけですが、すると、少なくとも6本は同じ色になります。
というのは、同じ色が5本まで、だと、3色では15本までしか描けません。なので一番多い色は6本以上になるしかありません。16=6+5+5ですね。

では一番多かった話題を赤で描くことにします。また人（頂点）の並びも話題に応じて変えます。もともとは手紙のやり取りだから別に問題ないですよね。

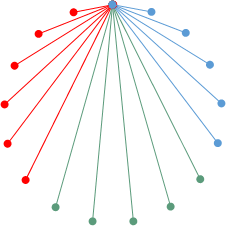
この先の（少なくとも）6人の間では、また互いに何かの話題がやりとりされているわけです。

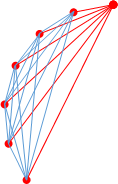
その先の部分を、とりあえず青で描いておきます。

この部分は6角形ですね。形を整えると

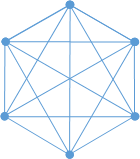
こうなります。

このどれかを赤で描くと、元の頂点からの赤2辺と組み合わせて、赤3辺の三角形ができあがってしまいます。そうしないためには、赤を使わずに、緑と青だけで全ての辺と対角線を描く必要があります。

※ここで振り返ってみると、元の問題は「17人で3つの話題」だったのが、「6人で2つの話題」に小さくなったことがわかります。

ではここから先も、同じ考え方で進めましょう。

１つの頂点に注目すると、相手は５つです。

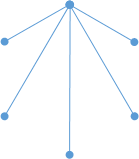
これを2色で描き分けると、最低3本は同じ色になります。2本＋2本だと4本にしかなりません。5=3+2ですね。

では一番多い話題を緑で描きましょう。

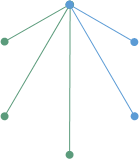
この先の（少なくとも）3人の間では、また互いに何かの話題でやり取りされているわけです。

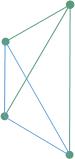
とりあえず青で描いておきます。

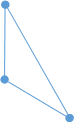
これを何色で描けばよいでしょう？　緑を使うと、先の頂点からの緑の2辺と組み合わせて緑の三角形ができてしまうので、緑は使えません。

となると、もう青しか残っていませんが、全部青だと、ここで青による同色三角形ができてしまいます。

もちろん赤を使っても、最初の頂点からの2辺と組み合わせて赤の三角形ができてしまいます。

というわけで、どうしても同色三角形ができてしまいます。（証明終わり）

こうしてみると、「17」という数字は、この証明のためのギリギリの数字だということもわかりますね。

17=1+16

16=6+5+5

6=1+5

5=3+2

問題を解くときは上から下に辿ってきましたが、下から上に遡ると、3色の三角形なら17がギリギリだとわかります。

特殊な事前知識を全く必要とせず、また、複雑に見えても順番に解きほぐしていくと実は単純、という、なかなか素敵な問題でした。

【おまけ１】

どうやってこの解法を思いついたか？について簡単に説明します。

まず問題の内容を明確化し、さらにそれをイメージ化しました。それによって、そこからいろんな連想をすることができます。

次に、なぜ「少なくとも6本は同じ色」に注目したか？ですが、実はここがポイントなのかもしれません。それまでは元の問題と「同値」あるいは「必要十分条件」で考えを進めていましたが、それ以上は先に進めなさそうなので、「少なくともこれは言える」という、いわば「十分展開」（造語です）に切り替えました。ダメだったらその時は他の道を探そう、ということです。で、まあ、人数が多い方が同じ話題で重複しやすいだろう、と、まずはその方向で考えてみました。結局そのままスムーズに解けたわけですが。16=6+5+5の時点で、ちょうどギリギリの数字だったので、なんとなく行けそうな気がしました。

【おまけ２】

このような階層構造を見せられると、逆方向に展開したくなります。つまり「話題が４つだったら、何人以上で3人組が発生すると言えるか？」という発展問題です。さらに、「話題がn個のとき、何人なら同じ話題の3人組が発生すると言えるか？」という一般化も簡単にできそうですね。

ただし、上の方法で示せるのは、厳密には上限値でしかありません（最小値ということを証明したわけではありません）。その人数より一人少ない場合は、ここの証明方法では「何とも言えない」からです。

【おまけ３】

正17角形の図を拾って来ようとネットで検索したら、定規とコンパスで作図できるらしいですね...。19歳のガウスやばい...。とはいえ、実際に定規とコンパスで作図しようとしても、すぐに誤差が乗って大変そうですが、おかげで正17角形の画像は簡単に見つかりました。ありがとうガウス。